Bí ẩn tỷ lệ vàng

Ф và Bí mật của vẻ đẹp hài hòa

Tỷ lệ vàng khi được áp dụng trong nghệ thuật đều mang đến cho con người 1 cảm giác đẹp hài hòa và dễ chịu một cách khó giải thích. Do đó, nó được giảng trong các môn học như nghệ thuật, kiến trúc, mỹ thuật, trang trí, hội họa, điêu khắc, nhiếp ảnh, vv… như là một quy luật, tương hợp kỳ lạ với óc thẩm mỹ tự nhiên của con người.

Apple vận dụng tỷ lệ vàng trong các thiết kế của mình, ngay cả trang Twitter cũng vận dụng nó, các mẫu logo của các công ty hàng đầu thế giới cũng áp dụng tỉ lệ vàng. Tờ báo mà bạn đang đọc, màn hình vi tính, thẻ tín dụng, toà nhà cao ốc, cánh hoa, lá cây – tất cả mọi thứ đều được tạo lập dựa trên một nguyên tắc, một tỷ lệ, một giá trị cân đối. Dường như Tạo hóa đang tiết lộ với chúng ta về bí mật của bản thiết kế mà Ngài đưa vào trong mỗi phần tử của vũ trụ.

Qua nhiều thế kỷ, cái đẹp tuyệt đối của nghệ thuật và óc thẩm mỹ của loài người chưa bao giờ chệch quá xa khỏi tỷ lệ kỳ bí này.

Vẻ đẹp của cơ thể con người cũng có liên quan tới số Ф. Thương của phép chia chiều cao từ đầu tới chân với khoảng cách từ rốn tới chân ≈ 1.618, thể hiện sự hài hoà cân đối của cơ thể. Chúng ta cũng có thể tìm ra kết quả tương tự trong tỷ lệ của chiều dài cái đầu với khoảng cách từ mắt tới cằm; hay tỷ lệ của khoảng cách từ mũi tới cằm trên khoảng cách từ môi tới cằm. Những tỷ lệ của gương mặt càng tiến gần tới tỷ lệ này thì gương mặt càng hài hoà cân đối. Thậm chí sở thích của chúng ta dường như cũng đã được định sẵn.

Trong một cuộc nghiên cứu nổi tiếng do Gustav Fechner tiến hành năm 1876, trong đó người ta được yêu cầu chọn một hình chữ nhật ưng ý nhất trong số một bộ các hình chữ nhật có kích thước từ một vuông đến gấp đôi. Kết quả là kích thước hình chữ nhật càng gần với hình chữ nhật vàng thì số người lựa chọn càng tăng lên. Ông còn nghiên cứu xa thêm bằng cách đo đạc tỉ lệ của các cửa sổ và cửa ra vào của các ngôi nhà, và phát hiện phần lớn chúng xấp xỉ tỉ lệ vàng. Điều đó cho thấy óc thẩm mỹ đã đưa nhân loại đến gần tỉ lệ vàng mà bản thân họ cũng không biết.

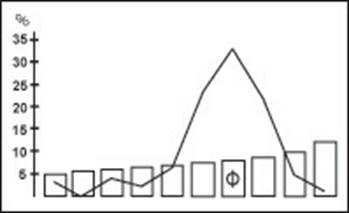
Tỉ lệ các cạnh của hình chữ nhật càng gần Ф thì càng bắt mắt.
Hình chữ nhật có chiều dài / chiều rộng = Ф được gọi là hình chữ nhật vàng

Cả loài người vẫn không thể giải thích được tại sao vô số những thực thể hữu cơ lẫn vô cơ tìm thấy trong tự nhiên lặp đi lặp lại tỷ lệ đặc biệt trên. Nguyên nhân đằng sau con số chi phối sự cân đối hài hoà và vẻ đẹp của toàn thể vũ trụ và nhân loại ấy là gì? Câu hỏi này đã thu hút sự quan tâm đặc biệt của rất nhiều người trong hàng thiên niên kỷ qua, nhưng cho đến ngày nay nó vẫn tiếp tục là một điều bí ẩn.

Ф và các công trình kiến trúc

Tỉ lệ vàng đã được áp dụng trong các kích thước kiến trúc của các công trình nổi tiếng như đền Parthenon Hi Lạp, các kim tự tháp Giza và thậm chí của cả tòa nhà trụ sở Liên hợp quốc tại New York. Một số kiến trúc Việt Nam cũng thể hiện tỉ lệ này.

“Thước tầm” thời xưa của Việt Nam với những số đo xuất phát từ các kích thước của con người cũng tuân thủ quy luật của Tỷ Lệ Vàng. Tỉ lệ giữa “khoảng nằm” và “khoảng đứng” luôn là một số ≈ Ф, mặc dù con số ấy có sai khác đôi chút giữa các phường thợ khác nhau.

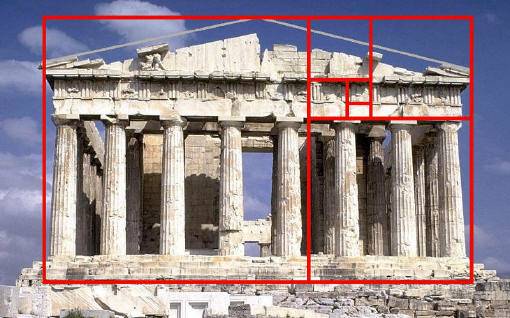
“Hình chữ nhật vàng” trong thiết kế đền thờ Parthenon tại Hy Lạp

Tháp CN tại Toronto, Canada là tòa tháp cao nhất thế giới, cũng được thiết kế theo tỉ lệ vàng. Tỉ số giữa tổng chiều cao tháp so với độ cao của đài quan sát là 553,33m : 342m = 1,618 = Ф

Kiến trúc tuyệt mỹ của thế giới –Taj Mahal– xây năm 1648, cũng chứa trong nó tỉ lệ vàng

Tháp Rùa, Hà Nội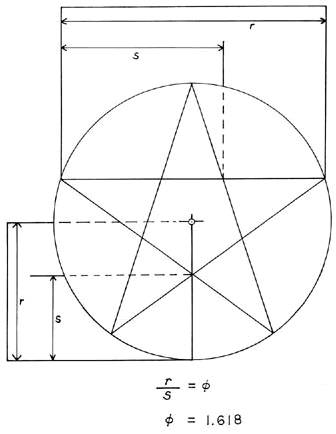

Một công cụ hay được dùng trong nghiên cứu và ứng dụng Tỉ lệ vàng là chiếc compa Tỉ lệ vàng.

 
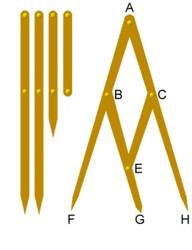
Compa tỉ lệ vàng. Ta có ABEC là hình bình hành, nên FG/GH=FB/BA= Ф

Một số kiến trúc khác có thiết kế phù hợp với tỉ lệ vàng:

Ф và Quy tắc phần ba trong nhiếp ảnh

Hằng số Ф chi phối hầu như mọi thiết kế của tự nhiên nói chung và các sinh thể nói riêng, tạo ra vẻ đẹp hài hòa. Tỉ lệ vàng là một khuôn mẫu đã đi vào sách vở và vẫn được giảng dạy cho đến ngày nay, do đó việc người ta áp dụng nó trong nhiếp ảnh là một điều dễ hiểu.

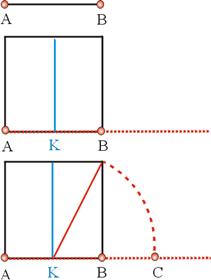
Cách dựng “hình chữ nhật vàng”

Trong nhiếp ảnh, người ta thường nói đến quy tắc phần ba: 1+0,618+1.

Các nhiếp ảnh gia giàu kinh nghiệm đều biết Tỉ lệ vàng trong việc sắp xếp bố cục, và sử dụng chúng nhuần nhuyễn một cách gần như tự động, không phải suy nghĩ. Nhưng trước khi đạt được đến trình độ ấy thì họ thường phải học hỏi và luyện tập nhiều. Dưới đây là một số bức ảnh chụp có sử dụng quy tắc này.

Khi càng đặt nhiều đường “Phi” trùng với các đường nét chính của chủ thể, thì tính hấp dẫn càng cao hơn

Như với thí dụ trên, con mắt của con ngựa được đặt ngay một “giao điểm” của “Phi”.

Một ví dụ khác, với hình trên, cách bố trí điểm “Phi” được đặt ở ngay mắt trái của chủ thể, để tạo chủ điểm hấp dẫn.

Đường chân trời được đặt ngay tại đường “Phi” trên, ngôi nhà thờ, và con đường tạo mối liên kết với nhau

Lịch sử bí ẩn của Tỉ lệ Thần thánh

Franziskanermönch Luca Pacioli di Borgo San Sepolcro (1445 – 1514) – một giáo viên toán ở Perugia, đã gọi tỉ lệ này là Tỉ lệ Thần thánh (“De Divia Proportione”) và cho ra đời 3 cuốn sách vào năm 1509. Trong cuốn đầu tiên ông chỉ nêu các vấn đề toán học. Trong cuốn thứ hai ông nêu ra sự liên quan giữa bản viết của một người La Mã là Vitruvius từ thế kỉ 1 trước công nguyên với Kiến trúc, trong đó còn nói về việc lấy tỉ lệ người như là một khuôn mẫu.

Adolf Zeising (1854) đưa ra mối liên quan giữa tỉ lệ vàng và Nghệ thuật. Ông tin chắc rằng mọi vật thể sống đều tuân theo một qui luật tự nhiên về thẩm mỹ, mà cơ bản ở đây là tuân theo Tỉ lệ vàng. Ông đã tìm kiếm và nhận thấy rằng tỉ lệ vàng có ở khắp mọi nơi. Nghiên cứu của ông đã gây tiếng vang lớn trong dư luận.

Martin Ohm (em trai của George Simon Ohm với định luật Ohm nổi tiếng) từng đưa Tỉ lệ Vàng vào giảng dạy trong một giáo trình toán. Cụm từ sectio aurea (tỉ lệ Thần thánh) cũng được đưa ra trong thời kì này.

Vào những năm đầu thế kỉ 20 xuất hiện một bài viết về quan sát tỉ lệ vàng của một người Rumani tên là Matila Costiescu Ghyka. Ông đã kết hợp giữa lý thuyết của Pacioli và nghiên cứu về thẩm mỹ của Zeising và kết luận Tỉ lệ vàng như là một bí ẩn của vũ trụ, xuất hiện khắp mọi nơi.

Trước đây người ta vẫn cho rằng một người La Mã là Vitruvius sống cách đây gần 2.100 năm đã phát minh ra tỉ lệ vàng. Tuy nhiên Tỉ lệ Vàng đã được tìm thấy trong các kiến trúc cổ xưa hơn nhiều, ví dụ Kim tự tháp Lớn của Ai Cập.

Cho đến ngày nay nhân loại vẫn không biết kiến thức về Tỷ lệ Vàng có từ bao giờ.